科普

Pi 是永恆 (一)

David Yu4 Comments

亞視永恆。但有些東西可以比亞視更永恆。

我們都學過圓周率，而且我們都知道圓周率的名字叫做 \pi。在學校裡，我們必定學過一條公式，就是如何用一個圓形的半徑去計算它的周長，即是圓周：

C=2\pi R。

上式告訴我們「圓周 C 除以兩倍半徑 (即直徑) 2R 等於 \pi」，大概就是我們對 \pi 的第一個印象吧！我們在學校也學過，上式中的 \pi 是一個常數。換句話說，無論一個圓形有多大，它的圓周 C 和直徑 2R 之間的比例都是不變的。

有史記載第一個證明 \pi 是常數的人，有說是阿基米德。他使用極限 (limit) 的數學概念，以逼近法把 \pi 好像夾三文治一樣夾出來！從而證明它是一個常數，計算出 \pi 在 3.1408 和 3.1429 之間，準確至兩個小數位。事實上，\pi 是無窮無盡的，即是它擁有無限個小數位，怎樣計也永遠計不完。現代的超級電腦，可以把 \pi 計算至萬億個小數位。可是，萬億個小數位距離無限，仍然是無限遠。

我們知道這些都是事實。可是，我們又有沒有想過，為。什。麼？

在這一連幾篇文章中，我會用兩個不同的方法去證明 \pi 是一個常數，即是證明所有圓形的圓周率都是一樣的。換句話說，我們會證明所有圓形的圓周與直徑的比例都是一樣的。然後我會介紹其他與圓形和 \pi 有關的問題和故事。好了，我們開始吧！

首先第一個證明，涉及微積分的概念。注意在此證明之中我並不會用到實際微積分的運算技巧；使用微積分的符號只為證明的完整和方便而已。未學過微積分的讀者不用太過在意，只需要知道記住「積分」只是計算無限短的長度的加法，而「微分」可想成是積分的反向操作而已。 (也可參考上回，微分是計算無限短線段的斜率的方法)

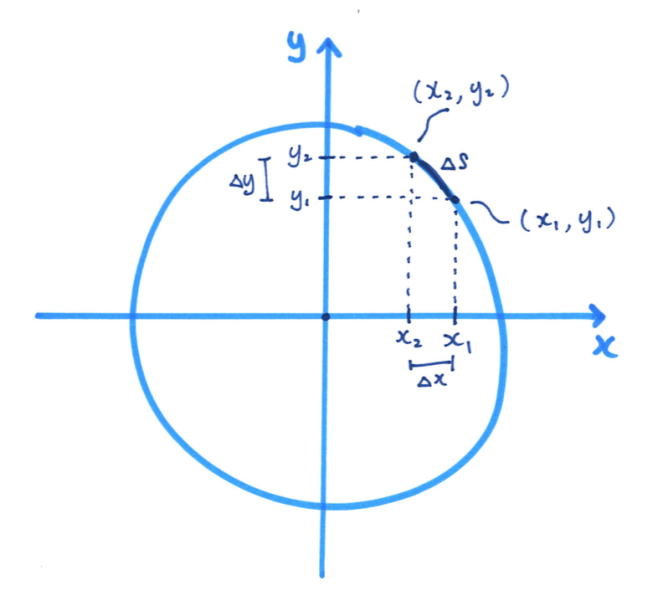
首先，我們有一個半徑為 R 的圓，圓心 O 點放在 (x, y) = (0, 0)。現在於圓形上任意選擇一段長度為 \Delta s 的段落。\Delta s 兩端對應的座標叫做 (x_1, y_1) 和 (x_2, y_2)。如下圖：

Screen Shot 2015-12-16 at 15.11.11

我們問，\Delta s 有多長？假設我們選擇的 \Delta s 非常非常短。當趨向於無限短，那麼 \Delta s 就差不多是一條直線。根據上圖，使用我們討論過的畢氏定理，我們就有 \Delta s= \sqrt{\Delta x^2 + \Delta y^2}。明顯地，如果把很多段 \Delta s 圍繞圓心加起來，就會等於圓周的長度。把很多段無限短的長度加起來的方法，就叫做積分，符號上是這樣寫的：

S=\int \textrm{d}s=\int\sqrt{\textrm{d}x^2+\textrm{d}y^2}。

把 \Delta 寫成 \textrm{d} 是為了表示無限短的意思，只是微積分的慣用符號而已。上式可寫成

S=\int\textrm{d}s=\int\sqrt{1+\left(\frac{\textrm{d}y}{\textrm{d}x}\right)^2}\textrm{d}x。

這公式告訴我們如何計算任意一段線段的長度。這公式不單止適用於圓形，也適用於所有能夠定義斜率 \frac{\textrm{d}y}{\textrm{d}x} (即是高度除長度) 的線段。所以現在我們只需要知道圓形的 \frac{\textrm{d}y}{\textrm{d}x} 就可以計算圓周長度了。懂得微積分運算的讀者可以自行快速計算，但我說過此文中我會不用微積分運算。那麼要如何做呢？原來非常簡單，只需要知道初等幾何學裡的一個定理：兩條互相垂直的直線的斜率相乘等於 -1。

Screen Shot 2015-12-16 at 15.17.40

見上圖，沿半徑方向的斜率明顯等於 \frac{y}{x} (其實就是斜率的定義而已)，而我們希望找到的沿圓周方向的直線 (即是圓周上的切線) 與半徑互相垂直，所以

\frac{\textrm{d}y}{\textrm{d}x}\times\frac{y}{x}=-1，

因此圓周的斜率就是

\frac{\textrm{d}y}{\textrm{d}x}=-\frac{x}{y}。

把上式放回積分裡，就有

S=\int\sqrt{1+\left(\frac{-x}{y}\right)^2}\textrm{d}x，

把開方裡面通分母再化簡，就得到

S=\int\frac{R}{y}\textrm{d}x，

在《畢氏定理 X 圓 X 三角學》裡，我們已經知道 y = R\sin\theta。所以

S=\int 1 / \sin\theta\textrm{d}x。

現在我們有一個問題，就是要把很多段 1 / \sin\theta 加起來，但是其長度卻用 \textrm{d}x 去表達。就正如計算面積時，我們不可以用米做高度、厘米做長度，單位必須一致。怎麼辦呢？不用擔心，只需要知道每個 \textrm{d}x 等於多少個 \textrm{d}\theta 就可以了！就如只需要知道一米有多少厘米一樣。

在《畢氏定理 X 圓 X 三角學》裡，我們也知道 x = R\cos\theta。所以我們要知道的就是：當 \theta 改變少許的時候 x 改變多少？心水清的讀者已經知道，這正正就是上回講到的斜率了，只不過由計算 \frac{\textrm{d}y}{\textrm{d}x} 變成計算 \frac{\textrm{d}x}{\textrm{d}\theta}，概念一樣。而且從上回的討論中我們已經知道 cosine 的斜率就是負 sine，因此

\textrm{d} x = - R \sin\theta \textrm{d}\theta。

原來每個 \textrm{d}x 等於 - R \sin\theta 個 \textrm{d}\theta。所以我們就知道

S=\int -R\textrm{d}\theta。

不論 \int -\textrm{d}\theta 等於多少，也與 R 無關。因此圓周上任意長度 S 與直徑的比例就是

S/2R=\int -1/2\textrm{d}\theta，

只與角度 \theta 有關。因此無論圓形有多小多大 (由 R 一個變量決定)，此比例亦恆等不變。所以我們就證明了無論一個圓形有多大，它的圓周 C 和直徑 2R 之間的比例都是不變的！

最後，我們來證明這個數字等於 \pi。其實這也不可以說是一個「證明」，只是一個定義 \pi 的方法罷了。不過有了這個定義，下回我們就可以計算 \pi 的數值。數學上，我們習慣把角度的 180 度叫做一個 \pi。繞圓周轉一圈是 360 度，所以半個圓周周長就是把上式由 0 度積分至 180 度，即是由 0 積分至一個 \pi：

(C/2)/2R=\int^{\pi}_{0} -1/2\textrm{d}\theta = -\pi/2。

上式中的負號是因為我們在上面作開方根的時候，沒有考慮正負兩個選擇。長度當然不能是負數，因此這告訴我們在上面的開方步驟中應該選擇負的結果。所以上式就說「半個圓周 C/2 與直徑 2R 的比例是 \pi/2」。換句話說，

C=2\pi R。

\pi 是永恆。下回，我們來看看它如何能夠 loop 到下個世紀，仲未埋尾。

延伸閱讀：

《三角 X 斜率 X 微積分》- 余海峯

《畢氏定理 X 圓 X 三角學》- 余海峯

《加菲證明畢氏定理》- 余海峯

4 thoughts on “Pi 是永恆 (一)”

  3. 圆周率是定值这一点是欧氏几何的特征，在其他类型的几何里，比如双曲几何，圆周长与直径的比值不一定是一个常数。

    Like

    Reply

Leave a reply to Pi 是永恆 (二) – 余海峯 David | 物理喵 phycat Cancel reply